 |
 |
| Aus der Flugpraxis entwickelte theoretische Abhandlungen über: |
 |
|
|
 |
|
|
 |
|
|
 |
 |
|
|
 |
 |
|
|
|
Servohebel  Gestänge Gestänge  Ruder Ruder
|
Was steckt hinter dem Wort Stellmoment? Und ist es eigentlich egal, in welche Bohrung des Servo- oder Ruderhebels man das Gestänge einhängt? Beim Versuch diese Fragen zu beantworten, kommt man vom Hundertsten ins Tausendste und zu erstaunlichen Erkenntnissen!
Dass man für kleine, leichte Modelle ebensolche Servos einsetzt und für große, schwere Modelle entsprechend kräftige, leuchtet ein. Bedenkt man jedoch, dass Pylon Racer die 300 km/h Marke überschreiten und Jet-Modelle die 400 km/h Marke, sollte man sich über die hier behandelte Problematik schon Gedanken machen.
Betrachtet man den Gesamtkomplex Rudermaschine-Servohebel -> Gestänge -> Ruder-Ruderhorn, wird schnell klar, dass nur fundiertes Wissen um die physikalischen Zusammenhänge der Wegweiser zum Erwerb einer maßgeschneiderten Rudermaschine sein kann.
Hier sprang helfend Dipl. Ing. Claus Hohmann / BRD ein. Durch Jahrzehnte in der Luftfahrtindustrie beschäftigt und bekannt durch seine herausragenden technischen Abhandlungen in der Zeitschrift FMT, überließ er zu diesem Thema dem Schreiber dieser Abhandlung nicht nur seine Unterlagen nebst Grafikanregungen zur Benützung. Auch beantwortete er in der Folge bereitwilligst, geduldig und wiederholt Zusatzfragen. Für all dies und die Durchsicht des Manuskriptes großen Dank.
Technische Abhandlungen kann man nicht einfach überfliegen
Jugendliche, die nicht oder noch nicht Physikunterricht genossen oder erleiden mussten, oder andere, die das einst Erlernte schon längst vergessen haben, aber die Ableitungen der wenigen, hier vorkommenden einfachen Formeln wissen möchten, müssten den Lehrstoff Physik/Mechanik/Bewegung (Kinematik) für 4. Klassen allgemein bildender höherer Schulen auffrischen.
Als Beispiel: ist Gewicht gleich Kraft? Legt man einen Gegenstand auf die Waage oder hängt ihn an einen Kraftmesser, so kann zufällig 1 kg angezeigt werden. Wegen der Erdanziehung gilt, dass eine Masse von 1 kg (das kann ein Goldnugget aber auch ein großer Block Styropor sein) an einem Normort (Zürich oder Paris) ein Gewicht von 9,81 Newton (N) hat. 1 Newton (N) gilt also als Maßeinheit für jene Kraft, die die Masse m von 1 kg vom Ruhezustand beginnend, innerhalb 1 Sekunde auf eine Geschwindigkeit von 1 Meter pro Sekunde bringt. Diese Beschleunigung erfolgt im Quadrat der Sekunde. Die Kraft die also einem Kilogramm kg diese Beschleunigung von 1 m/s² erteilt, nennt man Newton (N). Daher die Benennung Kraft, anstelle Gewichts. Zuweilen liest man auch Gewichtskraft (grob: 1 kg = 10 N).
|
| Spätestens hier endet der Artikel für Leser von Clubnachrichten oder den nur an Modellbau Interessierten. |
| Wissbegierige Modellflieger werden diese Arbeit sicher sorgfältig lesen bzw. studieren. |
| Für ungeduldige Praktiker: die Quintessenz einfach den gelb unterlegten Zeilen entnehmen. |
|
Stellmoment, Haltemoment
In technischen Daten zu Rudermaschinen scheint unter anderem auch das Stellmoment in Newtonzentimeter (Ncm) auf und bei Digitalservos auch das Haltemoment in (Ncm). Schon seltener der Drehbereich des Servohebels (°).
Die Definition des Stellmoments, physikalisch Drehmoment, ist allgemein: MD = F * R [1]. Darin ist F die Kraft in (N) und R die Länge des Ruderhebels in (m). Für Berechnungen muss R immer im rechten Winkel zu F stehen!
|
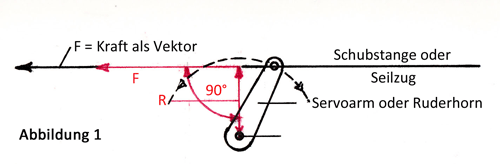 |
In nebenstehender Abbildung 1 wird die Kraft F (N) einer Rudermaschine über die Länge eines drehbaren Servohebels R (m bzw. cm) zur weiteren Ausnützung auf das Gestänge (Schubstange oder Seilzug) übertragen. (Die Wirkrichtung wird Vektor genannt. D. h.: die Kraft F hat keinen festen Platz und kann beliebig verschoben werden. Die Wirkung bleibt immer gleich). |
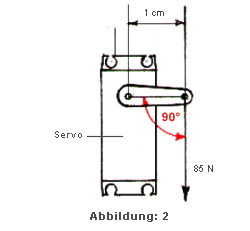 |
Erläuterung der Normangaben (Ncm) aus Abbildung 2:
hängt man an einen 1 cm langen Servohebel z.B. des C 4421-Normalservos (bei 5 Zellen-Akku!) ein Gewicht von 85 N, so hält das Servo diese 85 N in Position und kann das Gewicht von 85 N auch hochheben = 85 Ncm (lt. Herstellerangaben).
Anders verhalten sich wegen des aufwendigeren, technischen Aufbaues Digitalservos: das DS 8411 z.B., kann bei 1 cm Hebel 115 N heben (Stellmoment), jedoch sogar 180 N halten (Haltemoment).
Stellt man die Gleichung [1] um, so ist F = MD / R und R = MD / F. Halbiert man bei gegebenem Servo den Lochabstand (Servodrehachse zu Gestängeloch 90° zu Kraftvektor) von 1 cm auf 0,5 cm, dann ist F = 85 / 0,5 = 170 N. Vergrößert man diesen Abstand jedoch auf 1,5 cm, dann ist F = 85 / 1,5 = 56,66 N. Die Gestängekraft F verkleinert sich nun bei immer gleich bleibendem MD um 66%.
|
| Für den Praktiker: Verkleinerung des Servohebel - Lochabstandes vom Drehpunkt unter 1 cm bedeutet Vergrößerung der Gestängekraft. Erweiterung über 10 mm ergibt Verringerung der Gestängekraft, bei unverändertem Drehmoment! |
|
|
Drehbereich, Servoweg, Gestängekraft
Der Servodrehbereich wird lt. Katalog beim C 4421 mit 2 mal 43° angegeben. Das ist die Normaleinstellung bei 100% Servoweg des Senders. Wird dieser auf 150% verstellt, so vergrößert sich der Servohebelvollausschlag auf 2 mal 58° (gemessen).
|
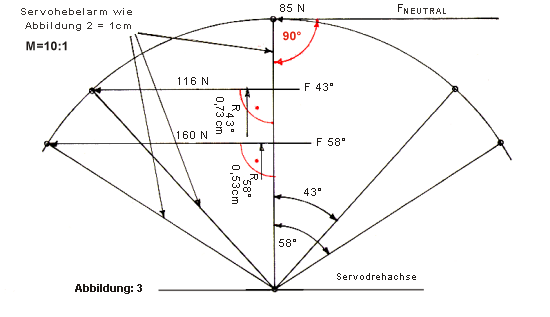 |
Aus Zeichnung 3, in stark vergrößertem Maßstab, erklärt sich eine sehr wichtige Erscheinung. Während der Bewegung des Servohebels tritt eine fortlaufende Änderung der Termen F und R aus Gleichung [1] ein. Der Hebelweg R wird immer kleiner, die Gestängekraft immer größer. Das Drehmoment MD, bleibt immer unverändert (die Stellkraft MD eines Servos wird von der dem Servo zugeführten elektrischen Energie bestimmt).
- Bei Neutralstellung ist R = 1 cm (senkrechte Gerade) und F = 85 N (obere Waagrechte)
.
- Bei 100% Vollausschlag mit 43° ist R jedoch nurmehr 0,73 cm, F dafür aber 116 N.
- Vergrößert man nun den Vollausschlag am Sender auf 150°, dann verkleinert sich im Endausschlag des Servohebels die wirksame Hebellänge R auf nurmehr 0,53 cm. Die Gestängekraft F hat jedoch bereits die beachtliche Größe von 160 N erreicht!
|
| Der Praktiker sollte beachten: im Bereich großer Servohebelausschläge (150%) sind kräftige Servos bei klemmenden oder blockierenden Rudern ohne weiteres fähig, schlecht montierte Ruderhörner loszureißen, zu schwache Gestänge zu knicken oder gar Billigscharniere zu zerlegen! |
|
|
Die Wahl der Bohrungen im Servo- und Ruderhebel
Um herauszufinden, in welche Ruderhorn- oder Servohebelbohrung man die am Ende eines Gestänges aufgeschraubten Gabelköpfe (Gestängeanschlüsse) einzuhängen hat, sollte man eine Zeichnung, ähnlich Abbildung 4, mit eigenen (aktuellen) Werten anfertigen.
|
 |
Dazu benötigt man außer einem Blatt Papier und einem spitzen Bleistift noch einen Zirkel, einen Winkelmesser und einen Maßstab.
- Zuerst zeichnet man nach Bauplan, Eigenentwurf oder vorhandenem Modell einen Tragflächenquerschnitt in Originalgröße. Servohebel und Ruderhorn in Neutralstellung. (Eine gerade Linie tut es auch)
Spätestens jetzt sollte man sich über die Größe des individuellen Rudervollauschlages im Klaren sein. Im Beispiel wurden 25° gewählt. (Die für die verschiedenen Ruder erforderlichen Größen des maximalen Ruderausschlages sind Erfahrungswerte, oder in Beschreibungen angeführt).
- Je eine Senkrechte unter die Drehpunkte des Servos und des Ruders einzeichnen und beim Ruder beidseitig den gewählten Ruderausschlag (°).
Die Bohrungen des Ruderhorns befinden sich genau senkrecht unter dem Drehpunkt des Ruderblattes.
- Der Ruderhornradius RR ergibt sich aus dem Maß, bei dem sich die Stoßstange frei bewegen kann. Hier wurden 16 mm gewählt. (Praxisbeispiel: bei Vollausschlag 25° rechts des Ruderblattes und bei links angeschlagenem Ruderhorn: Gabelkopfloch im Ruderhorn so wählen, dass Stoßstange noch parallel zur Dämpfungsfläche verlaufen kann). Abstand R abmessen und einzeichnen und mit Zirkel die 25°-Schenkel schneiden.
- Jetzt wird der so entstandene Hub (Gesamtweg des Ruderhorns oder des Gestänges) am Ruderhorn bei R 16 ausgemessen. Im Beispiel = 13,5 mm.
Der Servoausschlag nach jeder Seite eines gerade zur Verfügung stehenden Servos beträgt laut Katalog 47°. Als Spielraum für kleinere Korrekturen beim Einfliegen nimmt man nur 42°.
- Diese 42° zeichnet man am Servohebel ein. Nur wenn das Servo wie vorher am Ruderhebel ausgemessen, den gleichen Hub von 13,5 mm geht, ist bei diesem Servoweg von 42° gewährleistet, dass auch der gewünschte Ausschlag von 25° am Ruderblatt zustande kommt. Also Hub von 13,5 mm einzeichnen.
- Nun kann man den Servoarmradius RS ausmessen und das benötigte Loch im Servorarm für den Gestängeanschluss wählen oder bohren. RS ist hier 10,1 mm (ach wie schön wäre es, wenn in den Säckchen mit den vielen Servohebeln oder auch bei den Ruderhörnern, wenigstens ein Exemplar dabei wäre, das keine Bohrungen, sondern nur eng aneinander liegende Körnungen zum Selbstbohren hätte. Die vorgegebenen Bohrungen passen selbst zu den in Baukästen beiliegenden Gestängen oder Anschlüssen selten).
Auf einem Bauplan im Maßstab 1:1 könnte man jetzt auch genau die Stoßstangenlänge ermitteln = Neutrallagen Servo- zu Ruderhebel.
Zugegeben, das hört sich alles ein bisschen lang an. Daher:
|
Für den Praktiker: im rechten Kästchen unter dem Ruderhorn der Zeichnung 4 ist die Formel zur Errechnung des Hubes eingetragen. Dafür benötigt man gewünschten Ruderausschlag in Grad und den Abstand RR von der Ruderachse bis zu gewähltem Ruderhornloch in mm.
Im linken Kästchen wird der erforderliche Lochabstand RS von der Servoachse errechnet. Bekannt muss lediglich der Vollausschlag des vorgesehenen Servos sein. Der Hub wurde ja schon errechnet.
Bitte keine Angst vor dem Sinus! Schon in einfacheren Taschenrechnern sind Winkelfunktionen programmiert. Probe: der Rechner ist richtig eingestellt, wenn man zuerst 30 (°) und dann sin drückt. Am Display erscheint als Ergebnis 0, 5 (In Worten: der Sinus von 30 Grad ist gleich 0,5)! |
|
|
Solange gewährleistet ist, dass sich das Gestänge nicht spießt, kann man natürlich das Pferd auch am Schwanz aufzäumen. Also rechtes Kästchen nach links verschieben und zuerst Hub beim Servo berechnen u.s.w..
Wie wäre es für den p. t. - Leser jetzt mit einer Probe aufs Exempel? Man nehme ein eingeflogenes Modell und geht nach obigen Angaben vor um herauszufinden, ob gemurkst wurde!
Noch eine Warnung: würde sich während des Einfliegens herausstellen, dass der Ruderausschlag, wie im Beispiel, von 25° zu groß gewählt wurde und daher eine Wegverkürzung des Servos über die Senderelektronik auf nur 12° vorgenommen wurde, entstehen, wie man aus dem vorher aufgezeigten Vorgängen entnehmen kann, erhebliche Probleme. Durch Verkürzung des Servolaufes wird nicht nur das Servo mechanisch höher belastet (Abb. 3). Auch die Positionsgenauigkeit des Ruders wird nahezu halbiert, was zu einem wellenförmigen Geradeausflug führen kann. In diesem Fall: nochmals Papier, Bleistift und Zirkel bemühen und neu zu zeichnen beginnen. Danach Gabelköpfe neu positionieren. Dieses bisschen Mehrarbeit lohnt sich und geht mit der vereinfachten Zeichnung wirklich schnell.
Servostellkraft gegen Ruderdrehmoment
Man könnte diesen Absatz sehr kurz fassen, geht man von der Annahme aus, dass ein Großmodell mit 2 Quer-, 2 Höhenservos und einem Seitenservo, also 5 Jumbo-Servos ausgestattet ist. Sie wiegen zusammen 710 g. Der Servogewichtsanteil wäre dann bei einem 10kg-Modell 7,1% und bei einem 20 kg-Modell 3,5 %. Herr Hohmann empfiehlt daher, schon ab 10kg Modellgewicht, Großservos einzusetzen, da die Zunahme der Flächenbelastung gegenüber Normalservos maximal 3,5% beträgt. So gesehen, wäre nachstehende Rechnerei überflüssig.
Dessen ungeachtet soll im folgenden Abschnitt herausgefunden werden, welches Servo nach der Stellkraftangabe in Ncm tatsächlich imstande ist, die zu errechnenden Ruderkräfte zu bewältigen. Betrachtet werden Normalruder oder Klappen an Dämpfungsflächen. Pendelruder hingegen stellen einen Sonderfall dar, der einer separaten Abhandlung bedarf.
Erwartungen auf exakte Ergebnisse sollte man hier nicht zu hoch schrauben. Zu viele Variable spielen dabei eine Rolle. Auch hängt es von der Geduld und dem Genauigkeitssinn des Einzelnen ab, ob wirklich brauchbare Ergebnisse erzielt werden. Trotzdem: der gewissenhafte Modellflieger wird sich der Problematik stellen.
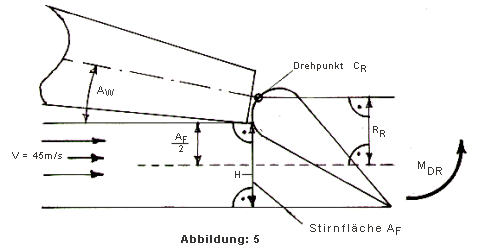
Man stelle sich eine Tragfläche vor, die aus Richtung V angeströmt wird. Der entsprechende Senderknüppel wird bewegt und die Rudermaschine beginnt, mittels ihrer Stellkraft MDS, die Muskeln spielen zu lassen und ein Ruder zu bewegen. Dabei baut sich an diesem Ruder mit dem Größerwerden der Anströmfläche AF ein Staudruck S auf, der im Endausschlag mit dem Hebel R um den Drehpunkt CR das maximale Drehmoment MDR bildet. Dieses Moment muss die Rudermaschine über die Stoßstange ST nicht nur bezwingen sondern auch halten.
Um nun die Strömungsvorgänge und das damit verbundene physikalische Kräftespiel zu untersuchen, bedient man sich am besten eines Rechenbeispieles.
|
 |
| Stirnfläche AF = H * L = 0,03m * 0,5m = 0,015m² |
| Staudruck S = Rho/2 * v² = 0,6125 * 2025 = 1240,3 N/m² |
| Ruderhebellänge RR = CR bis AF/2 = 2,5cm |
| Drehmoment MDR = ~ * MF * RR = 1240,3 * 0,015 * 2,5 = 46,5 Ncm |
|
Zeichnung 5 zeigt die angeführten Vorgänge an einem Tragflügelquerschnitt. Ein Profil wird unter einem x-beliebigen Anstellwinkel AW mit einer Geschwindigkeit V von 45 m/s (180 km/h) bei voll ausgeschlagenenem Ruder angeströmt. Errechnet soll das Ruderdrehmoment MDR werden, denn neben der geringen Bewegungskraft (bei leichtgängigen Rudern) muss ja das Servo vor allem diesem entgegenhalten. Weiter unten werden noch weitere Kriterien angeführt, die sich auf die Sollseite des Servos schlagen, aber der Übersicht und Vernachlässigbarkeit zunächst unbeachtet bleiben. |
| |
Als Ruderfläche AF gilt die senkrecht von der Strömung angeblasene Projektionsfläche. Im Beispiel: Höhe H = 0,03 m und Länge L = 0,5 m = 0,03 * 0, 5 = 0,015 m². |
| |
Der Staudruck S = ρ (Rho) / 2 * V² = 0,1249 / 2 * 45² = 0,0625 * v² = 126,43 kg/m² = 1240,3 N/m². |
| |
Das Drehmoment MDR [1] errechnet sich aus: Ruderfläche AF (m²) mal dem Staudruck S (N/m²) mal dem Radius RR in (cm), wobei für RR der Abstand vom Ruderdrehpunkt CR bis zur Mitte der Projektionsfläche (AF:2) gilt (hier 2,5 cm). MDR = 1240,3 * 0,015 * 2,5 = 46,5 Ncm. |
| Im Beispielfall würde man also mit einer Rudermaschine, die eine Stellkraft von > 46,5 Ncm aufweist, das Auslangen finden. (Eventuell Spannungsangabe (Zellenzahl) beachten). |
| Für maximale Servoausbeute gilt: Weg 150%, RSERVO möglichst klein und RRUDER möglichst groß = maximale Untersetzung. |
|
Um obige Rechnung nicht zu komplizieren, wurde der Soganteil hinter dem Ruderblatt (ähnlich den Vorgängen an der Druckanstiegsseite eines Profils) nicht berücksichtigt. Leider gibt es für den Bereich Modellflug hiezu keine genauen Untersuchungen bzw. Angaben. Nach Hohmann kann man dafür aus den Erfahrungen der Luftfahrt, Staudruck S * 1,3 einsetzen. Für obige Rechnung würde dann der Staudruck S statt 1240,3 immerhin 1612,4 N/m² betragen und das Drehmoment MDR = 60,5 Ncm. Bei großen und schnellen Modellen sollte dieses korrigierte Klappen- oder Rudermoment schon wegen eines Sicherheitsfaktors berücksichtigt werden.
Von den Faktoren für die Berechnung von MDR ist natürlich auch die möglichst genaue Bestimmung der Fluggeschwindigkeit erforderlich. Zum wiederholten Male kann hier nur festgestellt werden: solange nicht die vom Modell telemetrisch übertragene Fluggeschwindigkeit am Senderdisplay aufscheint, können darüber auch weiterhin nur Stoppuhr und Helfer auf einer genau ausgemessenen Messstrecke verwertbare Ergebnisse ermitteln.
Und genau genommen spielen beim 'Druck' auf das Ruder noch weitere Faktoren hinein. Nun mag die Kurvenbeschleunigung der Massenkräfte am Ruder, wie es der Physiker meint, bei Großflugzeugen eine nicht zu vernachlässigbare Größe darstellen. Ein Flugmodellruder wiegt ja nur wenige Gramm, dagegen ein Großflugzeugruder? Auch die Radialbeschleunigung beim Anfahren und Abbremsen der Ruderklappe kostet Kraft. Auch die durch fortschreitende Bewegung (Translation) entstehende Beeinflussung der Gestängemasse frisst Servostellmoment. Glücklicherweise scheinen all diese Faktoren, selbst bei großen Flugmodellen, vernachlässigbar. (Weitere mögliche Probleme: siehe prop 6/2002 Beitrag 'Rudervibrationen' von Rudolf Fiala).
Anders stellt sich die Angelegenheit im Großflug dar. Herr Hohmann berichtet aus der Geschichte der Luftfahrt, dass es wegen eines Fehlers in der Höhenrudertrimmung zu zwei Totalverlusten bei der Boeing 727 kam. Beim Erstflug der B 17 raste diese wegen eines ähnlich gelagerten Fehlers in einen Berg und beim Testflug einer VFW 614 entstand beim Test wegen eines Fehlers im gleichen Bereich ein Totalschaden (Gestänge arbeitete über den Totpunkt). Fehler in der Luftfahrt sollten aber Modellflieger wirklich nicht zu der Meinung verleiten: wenn denen schon solche Fehler passieren, dürfen wir uns dies allemal leisten.
Nun sitzen zum Glück in unseren Modellen keine Passagiere, weshalb die gerade angeführten Probleme im Bereich Modellflug häufig mit einem Achselzucken quittiert werden. Dass aber zumindest bei größeren und schnelleren Flugmodellen nach obigen Rechen- und Zeichenschema vorgegangen werden sollte, wird sicher durch die Umstände gerechtfertigt, dass man ja schließlich für das viele Geld und den nicht geringen Arbeitsaufwand, möglichst lange, Freude am Fliegen haben sollte. Noch schöner wäre es, würde diese Arbeit dazu beitragen, unnötigen Unfällen, hervorgerufen durch Fehler in der Ruderkinematik (Hineinrasen in Zuschauermengen), vorzubeugen.
|
| Erstveröffentlichung: Zeitschrift prop 2/2003
|
|

