'Sperber' - We 371

     Dass die Sinkgeschwindigkeitsrate bestimmter Antikflugmodelle weit hinter der heutiger Segelflugmodelle zurückbleibt, ist schon lange bekannt. Aus Erkenntnissen, von sich über Jahre erstreckenden, unzähligen Messflügen geht hervor, dass dafür die Vorgänge um die kritische Reynoldszahl Re_krit wohl von übergeordneter Bedeutung sind. Welchen praktischen Nutzen man aus dieser Erkenntnis ziehen könnte, behandelt in der Folge eine eingehende Studie.

     Etwa 1939 lernte ich eines der auf mich so ästhetisch wirkenden Modelle von Helmut Wechler* kennen. Mein Bruder baute damals den "Sperber" - We 371, ich selbst etwas später den Nurflügler "Silbermöve" - We 366. Die Flugleistungen beider Modelle blieben weit hinter den durch die Optik erweckten Erwartungen zurück. Trotzdem behielt ich diese Modelle in dauernder, nostalgisch verklärter Erinnerung.

Noch zu Beginn der Fünfzigerjahre wurden für die seinerzeitigen Flugmodellentwürfe bekannte Profile der Großfliegerei willkürlich ausgewählt, obwohl zu diesem Zeitpunkt bereits die Sinkgeschwindigkeitsmessung bei Wettbewerben Einzug gehalten hatte. Aus praktischen Baugründen waren es meist solche mit gerader Unterseite und vor allem mit entsprechender Dicke. Aus nebenstehender Vergleichsabbildung der beiden hier zur Sprache kommenden Profile ist unschwer zu erkennen, dass bei der geringen Strömungsenergie eines normalen Segelflugmodells (Fluggeschwindigkeit), sich dieses mit dem dicken, eben dieser Strömung beträchtlichen Widerstand entgegenbringenden Profils, recht "schwer" tun muß.

Ob sich bis heute jemand ernstlich der Mühe unterzogen hat, die gravierende Leistungseinbuße bei den Antikflugmodellen wegen dieser Profile (nicht alle!) durch Messungen im Flugvergleich mit modernen Modellflugprofilen nachzuweisen und die Ergebnisse auch zu veröffentlichen, ist dem Autor nicht bekannt. Dieser Beitrag berichtet von so einem Unterfangen, über die damit verbundenen Probleme und die sich darstellenden Erkenntnisse bzw. sich anbietenden Theorien!      An dieser Stelle sei aber zunächst ein kurzer Rückblick über die seit 6 Jahrzehnten andauernde Entwicklung in der Forschung der Aerodynamik des Modellflugs eingefügt.
     Zu Beginn der Modellfliegerei wurden zunächst ganz selbstverständlich die Erkenntnisse der Aerodynamik und Flugmechanik aus den diversen Forschungsanstalten für die Großfliegerei auch für den Modellflug übernommen. So weit dem Autor bekannt ist, erschien erst 1930 im "Flugsport" ein Bericht von Dipl. Ing. Walter Stender aus Breslau, in dem erstmals auf die unterschiedlichen Strömungsvorgänge zwischen Groß- und Modellflug ausführlich hingewiesen wurde. Diese Arbeit wurde, so scheint es zumindest, entweder nicht verstanden oder völlig ignoriert. Erst mit dem Erscheinen des Buches "Aerodynamik des Modellflugs" von F.W. Schmitz im Jahre 1942 über Tragflügelmessungen bei kleinen Geschwindigkeiten, wurden der Begriff und die Wichtigkeit der Re-Zahl wiederum einer breiten Modellflugöffentlichkeit zur Kenntnis gebracht. Dieses Buch schlug nun in interessierten Kreisen wie eine Bombe ein.
     Nun sollte man wissen, dass zu jener Zeit bei Wettbewerben keine wirkliche Leistungsanforderung an ein Flugmodell gestellt wurde, weder beim Hangflug noch im Hochstart. Wörtlich und recht kurz angebunden heißt es in den damaligen Startvorschriften: "Für die Zeitmessung gilt die Dauer des Fluges"! Sieger wurde also, dessen Flugmodell die längste Flugzeit erzielte. Egal, ob mit einem oder mehreren Starts. Erst mit Erscheinen des vorher genannten Buches kam so eine Art Leistungsdenken in der Modellfliegerei auf.
     Nicht zufällig war es dann die deutsche Kapazität auf dem Gebiet der Flugmechanik, Alexander Lippisch, der sehr bald nach Erscheinen des Schmitz´schen Buches diese Gedankengänge aufnahm. Der Begriff Profilgleitzahl, also der Quotient aus c_a / c_w, stand in seinen Ausführungen im Vordergrund. Er veröffentlichte daher Profile mit vermeintlich herausragenden Profilgleitzahlen aus den "geheimen" Technischen Berichten der Inspektion der Fliegertruppen, Charlottenburg anno 1917, die ihm für den Modellflug geeignet erschienen. Unerwähnt blieb, dass die Profilmesswerte auf Grund eines miserablen Turbulenzgrades des damals verwendeten Windkanals, illusorisch waren. Immerhin weckte auch er den Gedanken einer Leistungssteigerung des bislang wenig wissenschaftlich betriebenen Modellflugs, unter Bedachtnahme der Auswahl vermeintlich besserer Flügelprofile.
     Aus geschichtlicher Notwendigkeit sollte aber auch festgehalten werden, dass erst unmittelbar nach dem letzten Weltkrieg, so weit diese dem Autor bekannt sind, neben Benedek aus Ungarn, es vor allem Jedelsky und sein Mitstreiter Czepa aus Österreich waren, die den kategorischen Schritt wagten, völlig neue, keinen Turbulator erforderliche, und trotzdem überkritisch arbeitende Profile, die ausschließlich für den Modellflugbereich gedacht waren, empirisch aus Flugversuchen zu entwickeln. Den Weg dazu wies ihnen das "Fluggeschwindigkeitsprofil" der Natur, von der "Ebenen Platte" des Schmetterlings bis zum "Konkavprofil" des Greifvogels. Hand in Hand damit musste auch eine praktische Flugerprobung bzw. Messung erfolgen. So war es ebenfalls das Verdienst von Jedelsky/Czepa, die Sinkgeschwindigkeitsmessung für den Modellflug mit kurzer Hochstartschnur einzuführen (vom Autor dieses Beitrages wurde mit dieser Methode in mehr als zehn Jahren die Sinkgeschwindigkeit all seiner A2-[heute Klasse F1A] Seglerentwürfe exakt vermessen und das waren nicht wenige!). Man unterschied dabei sehr wohl zwischen den idealen Messbedingungen des Windkanals, ähnlich jenen in einer Halle mit seiner "idealen" Sinkgeschwindigkeit und jenen der freien atmosphärisch gestörten Flüge, nämlich der "Praktischen Sinkgeschwindigkeit".
    Dass so ganz nebenbei von ihnen Leistungsklassen bei Wettbewerben eingeführt und auch die Formen des bisherigen Flugmodells völlig umgekrempelt wurden, war nur eine Folge erstgenannter Bemühungen.
     Die wichtigste Innovation in der Aerodynamik des Modellflugs ist seitdem aber wohl zweifelsohne das Wissen um die grenzschichtnahen Strömungsvorgänge an unseren Flügelquerschnitten. Sie sind eng verbunden mit dem Namen W. Stender, F.W. Schmitz und K. Kraemer und jenen der Amerikaner Selig/Donovan.

     Für die eingangs angekündigten "Sperber"-Vergleichsmessflüge war es zunächst erforderlich, ein möglichst genau nachgebautes Originalmodell in Kiefer-Sperrholzbauweise und eine zweite Tragfläche gleichen Gewichtes und gleicher Oberflächenbeschaffenheit, mit einem erprobten, überkritisch arbeitenden Profilstrak zu erstellen. Fortan werden sie hier mit Modell 1 (Ursperber) und Modell 2 (mit neuem Profil) bezeichnet. Diese arbeitsintensive Aufgabe übernahm nun der in Niederösterreich lebende, überaus begeisterte, aktive Vertreter des Antikmodellflugs, Alfred Haiden. (Er baut auch Antikmodelle für das neu geschaffene Museum auf der Wasserkuppe!). Die Bilder dokumentieren sein Bemühen. Dank gebührt aber auch Alfred Haiden und seinen Freunden für die geleistete Hilfe bei den zeitaufwendigen Messflügen und den damit verbundenen Beschwerlichkeiten über viele, viele Monate.
    Zu den Modellen sei Folgendes angemerkt: Modell 1 und 2 unterscheiden sich lediglich durch zwei andersartig profilierte Tragflächen. Ein Rumpf mit Leitwerk dient beiden Variationen. Das Fluggewicht beider Modellkombinationen ist selbstverständlich ident.
     Das Wurzelprofil vom Modell 1 dürfte ein sogenanntes Kurvenlinealprofil sein. Jedenfalls entspricht es keinem der unzähligen Göttinger-Profile, die damals zum Einsatz kamen. Seine Dicke beträgt bei der Wurzel 14,47% und geht ab der V-Form in ein auf den Kopf gestelltes Clark-Y ähnliches Außenprofil von 11,25 % Dicke über (eine Art druckpunkfestes Nurflügelprofil), dessen Profilsehne gegenüber der des Wurzelprofils mit 5°! negativ eingestellt ist. Die endgültige Winkeldifferenz wurde bei diesem Modell auf +2°/ 0°, bezogen auf das Wurzelprofil, festgelegt.
     Beim Modell 2 wurde ein Re-Zahl bezogener Profilstrak (Dickenänderung), des bei vorliegender Gleitfluggeschwindigkeit v_x ~ 6,6 - 7,0 m/s (Annahmen: c_A = 0,9 - 1,0, G/F = 26,53 N/m² und Temperatur 20°) im gesamten Flügelbereich sicher überkritisch arbeitenden Profils, ähnlich dem S 4083, eingesetzt, mit einer EWD von 3,5°/0°. Zugrunde liegen dem: Flügelfläche 0,395 m², Fluggewicht 1069 g = 10,48 N und daher Flächenbelastung beider Modelle gleich 26,53 N/m². Schwerpunktänderung durch verschiebbaren Empfängerakku. Im Gegensatz zum Original sind Höhe und Seite natürlich ferngesteuert.
     Auch noch ein Wort zur Querstabilität des Freiflug- "Sperbers". Neben der notwendigen Erfüllung des vorgeschriebenen, heute riesig anmutenden Mindestrumpfquerschnittes L²/100 (L = Länge des Rumpfes), gebildet durch eine große vordere Rumpfseitenfläche einer vertikal stehenden Ellipse, glaubte man, den für den Hangfreiflug, und dafür war dieses Modell gedacht, unbedingt erforderlichen Geradeausflug, also die Richtungsstabilität, in den Griff zu bekommen. Eine Maßnahme , die wenig Wirkung zeigte, jedoch den Gesamtwiderstandsbeiwert c_W erheblich in die Höhe trieb. Auch viel V-Form war eine solche und auch wirksame. Gerade da aber mangelt es beim "Sperber" beträchtlich. Sie beginnt überhaupt erst bei 23,5% der Halbspannweite und ist mit 6,6%, bezogen auf die Spannweite, für Eigenstabilität unterdimensioniert. Üblich waren etwa 10% der Spannweite pro Flügelende, bei einfacher V-Form! Deshalb war das Modell schon damals um die Längsachse recht labil.
     Die Anregung zu vorliegenden Messflügen entstand eigentlich durch die alljährlich stattfindenden Antikmodellflugtreffen. Dort werden die alten Schmuckstücke allgemein mit Gummihochstart (30m Gummi plus 100 m Nylonseil) auf Höhe gebracht und eine bestimmte Maximalflugzeit gemessen. Nun allerdings ferngesteuert! Dabei stellte sich heraus, dass verschiedenste "Sperber" eine auffallend konstante Flugzeit von 2 min erbrachten, also eine vergleichbar miserable Sinkrate von 1,08 m/s. Das Einfliegen der vorher genannten Messmodelle bestätigte diesen Wert bei Modell 1. Das Modell 2 hingegen, mit dem neuen Profil, erbrachte eine Durchschnittsflugleistung von 3,5 min oder ein Sinken von 0,62 m/s.
     Eine Überschlagsrechnung prognostizierte für beide "Sperber", überkritischen Strömungszustand vorausgesetzt, mit einem angenommen hohen Gesamtmodellwiderstand von c_W = 0,09, einem c_A von 1,0 und der Flächenbelastung von 26,53 N/m², ein Sinken von 0,59 m/s. Tatsächlich wurde dieser Wert nur mit Modell 2 im 130 m-Gummihochstart mit 0,62 m/s annähernd erreicht. Da die 130 m Messungen nur dem Vergleich dienen, stellt sich erst gar nicht die Frage, ob die Ausgangshöhe von 130 erreicht wurde oder nicht, oder die Werte der Steigzahl c_W ² / c_A ³ bei der Berechnung der Sinkgeschwindigkeit korrigiert werden müssten. Es blieb einzig die Ursache des Mankos von 0,46 m/s! von Modell 1 zu Modell 2 aus den Vergleichshochstarts zu entschlüsseln. Was lag also näher, als diese in einem schlechteren Strömungszustand bei Modell 1 zu vermuten. Hier konnten nur Vergleichsmessungen Klarheit schaffen.
    Dazu sei ganz allgemein bemerkt: Versuche, den "Sperber" wie einst nur durch Laufen mit einem 18 m Nylonseil auf eine genaue Ausklinkhöhe von 20 Metern (einschließlich 2 m Handhöhe des Starters) zu bringen, scheiterten sofort an der verloren gegangenen Sprintfähigkeit der sich im fortgeschrittenem Alter befindlichen Läufer.
    Weitere Messflüge erfolgten nach langem Warten an einem ruhigeren Tag mit 5 m Rundgummi und 15 m Nylonschnur. Gewährleistet sollte wieder sein, wie bei der zuerst genannten Hochstartmethode, dass das Modell ohne Fahrtüberschuss oder Durchsacken in 20 m Höhe ausklinkt. Ein einziger großer Kreisflug sollte dabei das Modell wieder zur Startstelle zurückbringen. Ein fast aussichtloses Unterfangen! Die Streuwerte dieser Messflüge waren inakzeptabel.
     Wochen vergingen. Inzwischen wurde beschlossen, die Gummihochstartmethode wie vorher beschrieben, auf eine Ausgangshöhe von nur 10 m zu reduzieren. Dadurch konnte auf den Kreisflug, in Erwartung genauerer Messergebnisse, verzichtet werden.
     Und jetzt kam die große Überraschung! Bei den 10 m Hochstarts, erbrachten beide Flächen im Geradeausflug gegen den Luftstrom, nach wiederholten Messflügen, eine fast gleiche, allerdings auch viel zu gute Gleitflugleistung (unter 0,3 m/s)!
     Der Grund für die zu gute Flugleistung war wohl, dass bei der angewandten Gummihochstartmethode es fast unmöglich ist, eine konstante Ausklinkhöhe von zehn Meter zu erreichen. Trotzdem konnten wiederholt brauchbare Vergleichsstarts durchgeführt werden, da für beide Modelltypen die Ausklinkhöhe konstant blieb.
     Entscheidend für die nahezu gleiche Leistung beider Modelle bei ruhigen Luftverhältnissen dürfte der Flugzustand des ungestörten Geradeausfluges nach dem Ausklinken gewesen sein. Die Strömung verweilt auch an der Tragfläche mit dem dicken Profil, zumindest über einen Großteil ihres Grundrisses, gerade noch überkritisch anliegend. Hier könnte sich lediglich eine geringe Verschiebung der Sinkgeschwindigkeits-Leistung durch den unterschiedlichen c_a-Wert der Profile vom Originalmodell zu Modell 2 ergeben.
     Folglich konnte die Ursache des eingangs erwähnten, auffälligen Leistungsunterschiedes zwischen Modell 1 und 2 beim Hochstart mit 30m Gummi und 100 m Nylonseil gegenüber dem Geradeausflug, nur an anderen Strömungsvorgängen an der Tragfläche im Kreisflug liegen, worauf in der Folge näher eingegangen wird.
     Bei Strömungszuständen hoher Re-Zahlen (Re > 10⁶) geht man davon aus, dass die Grenzschicht der Strömung an der Tragflügeloberseite laminar verläuft. Bei Modellflügeln hingegen ist bei Re-Zahlen unter 100.000 (Re < 10⁵) der Grenzschichtzustand an der Saugseite völlig anders geartet. Nur wenn hinter dem Druckminimum* die bis dahin laminar anliegende Grenzschicht auf der Flügeloberseite, in eine turbulent anliegende Grenzschicht umschlägt, kann großer Auftrieb und kleiner Widerstand erreicht werden. (*Höchste Stelle des Profils: wandert mit steigendem Anstellwinkel nach vorn). Denn nur dieses Phänomen der turbulent anliegenden Grenzschicht ist imstande, den dort beginnenden Druckanstieg ohne Ablösung zu überwinden und auch nur dann, wenn die Reynoldszahl der Tragfläche größer ist als eine dem Profil eigene, kritische Re-Zahl. Man spricht dann von einem "überkritischen" zum vorher "unterkritischen" Strömungszustand. Für die kritische Re-Zahl eines Profils gibt es mehrere Kriterien. Hauptsächlich jedoch die Größe des Nasenradius, die Oberflächenbeschaffenheit und vor allem die Höhe seiner Oberseitenwölbung. Die kritische Re-Zahl Re_krit ist bei der ebenen Platte mit Re ~ 20 000 angegeben und beim Konkavprofil bis zu Re ~100 000.
     Zwar liegt für das im "Ur-Sperber" verwendete Profil kein Messbericht vor, doch geht aus der ausführlichen Arbeit "Flügelprofile im kritischen Reynoldszahl-Bereich" von Dr. K. Kraemer, Göttingen, folgendes hervor. An einem Endscheibenflügel mit dem Profil Gö 801, dessen Oberseitenwölbung mit max.11,8% noch weit unter dem vorher genannten Profil liegt (bei der Wurzel 14,7 %), ist bei konstantem, großen Anstellwinkel und kontinuierlich größer werdender Anströmgeschwindigkeit die Grenzschicht bis Re 61000 unterkritisch abgelöst und wird erst nach einem Übergangsbereich, genannt Hysteresis, bei Re 75000 überkritisch anliegend.
     Befasst man sich noch eingehender mit vorher Gesagtem, wird klar, welche Bedeutung dies alles für das Flugmodell kleiner Geschwindigkeiten und Flügeltiefen hat. Bei geringen Anströmgeschwindigkeiten (Flügeltiefen), bevor der Bereich der Hysteresis erreicht wird, also im unterkritischen Zustand, ist der Auftrieb c_A obige Messfläche 0,65 und der Widerstand c_W 0,095. Dieser bedauerliche Flugzustand tritt im Alltagsmodellflug eher selten auf, kann aber bei kleinen Schülermodellen (kleine Flügeltiefe, dickes Profil) zuweilen beobachtet werden. Nach der Hysteresis, im überkritischen Zustand, ist c_A 1,0 und c_W 0,039. Auf den Gleitwinkel arc tang φ = c_W / c_A umgerechnet bedeutet dies, dass dieser im unterkritischen Zustand 8,3 ° und im überkritischen 2,2° beträgt. Oder: ist im ersten Fall die Gleitzahl ε gleich 6,8, so ist sie bei turbulent anliegender Strömung 25,6! Erschreckend mutet die Gleitzahl des unterkritischen Bereiches von 6,8 an. Dann würde das Flugmodell bei einem Handstart in einer Entfernung von 13 Metern den Boden touchieren und das geschieht bei dem erwähnten Modellchen auch tatsächlich.
     Wie subtil darüber hinaus die beschriebenen Strömungsvorgänge sind, zeigt ein weiteres Beispiel. Bei einer Tragfläche mit 200 mm Flügeltiefe und dem Profil Gö 801 hält der unterkritische Strömungszustand bis zu einer Fluggeschwindigkeit von 4,4 m/s an, geht dann in den Hysteresisbereich über, um bei 5,4 m/s in den turbulent anliegenden, überkritischen Zustand umzuschlagen. Demnach bestimmt ein Geschwindigkeitsunterschied von lediglich 1,0 m/s, ob unser Flugmodell eine miserable oder gute Gleitleistung abzuliefern imstande ist. Oder, ob bei dieser Flügeltiefe die Flächenbelastung (gebildet aus Gewicht / Fläche) 12,0 oder 18,5 N/m² beträgt. In der alten Schreibweise ausgedrückt, können auch mickerige 6,5 g/dm² zwischen böse und gut entscheiden!
     Der unterkritische Strömungszustand wird oft mit abgerissener Strömung verwechselt. Der für die Großfliegerei (zuweilen auch bei Scale-Modellen) sich verheerend auswirkende Strömungsabriss, erfolgt beim Überziehen abrupt an der Flügelnase. Jeglicher Unterdruck an der Flügeloberseite geht dabei verloren. Hier helfen nur noch ein Gebet oder eine entsprechend große Höhe zum Abfangen.
     Anders beim Fehlen der turbulenten anliegenden Grenzschicht nach dem Druckminimum (höchste Stelle des Flügelprofils), also beim Übergang von der Hysteresis in den unterkritischen Zustand. Dort bleibt die Strömung von der Nase bis zu diesem Druckminimum noch laminar anliegend, was das Flugmodell, wenn auch mit miserabler Sinkleistung, zum Weiterfliegen befähigt. Erst bei zu großem Anstellwinkel erfolgt auch hier der totale Strömungsabriss.
     Nachfolgende Annahmen beziehen sich nun im Wesentlichen auf den Bereich der Hysteresis. In der Literatur als Übergangsbereich bezeichnet, dürfte er auch beim "Ur-Sperber" auftreten. Die mittlere Flügeltiefe t_m = F / b beträgt dort 0,2 m, die Fluggeschwindigkeit v_x ~ 7,0 m/s, die örtliche Re-Zahl Re-t_m demnach 98.000. Hier könnte man einen überkritischen Strömungszustand als sicher annehmen, zumal das Profil auf Grund des verwendeten Profilstraks an dieser Stelle (t_m) dem Gö 801 schon nahe kommt und die kritische Re-Zahl beim Gö 801 ja mit Re 61.000 angegeben ist. Dies wurde auch durch die oben erwähnten Geradeausflug-Messungen klar bestätigt. Zu bedenken ist jedoch, dass beim "Sperber-Grundriss" sehr wohl leider auch die kritische Re-Zahl Re_krit erreicht wird und zwar ab einer Flügeltiefe von 0,126 m, also im Außenbereich der Tragfläche. Auf diese Problematik, bei relativ spitz zulaufenden Flächengrundrissen, wird in der Literatur wiederholt hingewiesen.
     Dass der Kurvenflug auf die Strömungszustände am Modell einen negativen Einfluss ausübt, fände zunächst eine einfache Erklärung darin, dass die konstruktiv bedingte große, vertikale Rumpfform des "Sperber" beim Kurvenflug starke Interferenz-Verwirbelungen an den Tragflächenübergängen hervorruft (zusätzlich noch Flügelbefestigung mit Gummiringen an Dübeln), die sich auf die Tragfläche übertragen. Da dies aber Modell 1 und 2 gleichermaßen betrifft, ist dieses Argument für die Vergleichsleistung im Kreisflug nicht relevant.
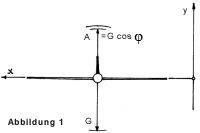     Daher erscheint folgende Überlegung zutreffender: Bei einem Flugmodell im stationären (unveränderten geradeaus) Gleitflug, ist der von der Tragfläche erzielte Auftrieb A gegenüber dem Gewicht G lediglich um den Kosinus φ des Gleitwinkels geringer, A = G cos φ (Phi) Abb. 1
     Anders sieht dies im Kreisflug aus. Während die Gewichtskraft des Modells als konstante Größe G in jeder Fluglage immer senkrecht und unveränderlich zur Erdoberfläche wirkt, steht die Auftriebskraft A immer senkrecht zur angeströmten Tragfläche, ihre Größe jedoch ist veränderlich und zwar in Abhängigkeit von der Größe des Kurvenneigungswinkels θ (Theta). Im Kreisflug ist also A um den Gleitwinkel φ nach vorn geneigt und durch den Schräglagewinkel θ zur Kreisachse.
     Im Gegensatz zum stationären Gleitflug (A = G cos φ), ist beim Kreisflug, wie die Auftriebskomponente in Abb. 2 zeigt, ein höherer Auftrieb A erforderlich. Dieser fehlende Auftrieb kann nur durch Ziehen am Höhenruder, also durch Anstellwinkelerhöhung ergänzt werden, soll das Flugmodell in etwa mit dem gleichen Gleitwinkel weiterfliegen wie im Geradeausflug. Damit also auch im Kreisflug der Auftrieb A wieder G cos φ wird, gilt nun A = G cos φ / cos θ.
[Abkürzungen zu Abb. 2: x ist die horizontale und y die vertikale Richtung. R der Kreisradius der Kreisebene, Zr die Zentrifugalkraft, G das Modellgewicht, A der Auftrieb, θ der Schräglagewinkel und φ der Gleitwinkel.]
     Aus den früher erwähnten Vergleichs-Messungen mit gleich guten Leistungsergebnissen kann hypothetisch angenommen werden, dass der "Ursperber" im ungestörten Geradeausflug in einem mittleren Flächenbereich überkritisch fliegt, jedoch ab einer Flügeltiefe von 0,126 m bis zum Flügelende sich im Hysteresisbereich befindet. Wegen seines sehr dicken Profils, allerdings mit einem größeren Auftriebskoeffizienten c_A der Tragfläche als Modell 2. Die gleich gute Leistung beider Modelle erklärt sich wiederum damit, dass Modell 2, wegen des wesentlich dünneren Profils wohl einen kleineren c_A-Wert aufweist, die Strömung sich jedoch nahezu über den gesamten Flügelbereich überkritisch verhält.
     Wie aus unten stehenden Rechenbeispielen ersichtlich, ist die erforderliche Auftriebserhöhung, die durch Anstellwinkel-Vergrößerung im Kurvenflug aufgebracht werden muss, bei der angenommenen Kurvenschräglage nicht all zu groß. Berücksichtigt man, dass der Auftriebsanstieg beim Gö 801 pro 2 Grad etwa 0,14 c_a beträgt, so entsprechen diese 2 Grad in etwa dem Auftriebsverlust bei angegebener Kreisflugneigung in Beispiel 1. Man kann also davon ausgehen, dass es bei der Höhenruderkorrektur allenfalls bei zu viel "Höhenruder", also zu großer Flügelanstellung, zu einem sicher sichtbaren Ablösen (Abriss) der Strömung käme. Andererseits bedeutet im Kreisflug zu wenig "Höhenruder", einen schnelleren Höhenverlust, und zwar umso mehr, je größer der Schräglagewinkel θ ist. Ganz allgemein wäre es also sehr ratsam, mögliche "flache" Kreise zu fliegen.
     Die Unterlegenheit beim Kreisflug des "Ursperber" von 0,46 m/s gegenüber Modell 2 würde sich demnach so erklären: selbst wenn die erforderliche Anstellwinkelvergrößerung beim gesteuerten, flacheren Kreisflug nicht all zu groß ist, könnte das erforderliche "Ziehen" von 2 Grad Mehranstellung dazu führen, dass wegen der kleinen Flügeltiefen im Außenbereich, sich der Hysteresisbereich dort über einen weiteren Bereich der Tragfläche ausbreitet, oder möglicherweise sogar das Flügelende unterkritisch wird.

Unter freundlicher Mithilfe von Dr. H. Quabeck ¹) Rechenbeispiele, für an Mathematik und Physik Interessierten, zur Findung der in Abbildung 2 gezeigten erforderlichen Auftriebserhöhung im Kurvenflug:
     Mit R dem Kreisradius, Zr der Zentrifugalkraft, muss im stationären Kreisflug Zr durch die Auftriebskraft Zr = A * sin θ * cos φ kompensiert werden. Für A gilt: A = θ / 2 * c_A * F * v² (mit c_A als Auftriebskoeffizient des Modellflügels, abhängig vom Grundriss. Wegen des elliptischen Grundrisses des "Sperber", hier c_A gleich dem c_a des Profils) und für die Zentrifugalkraft Zr in radialer Richtung der Kreisebene Zr = m / R * (v cos φ)². Je enger der Kreis und je steiler der Winkel θ, desto größer Zr. Daraus ergibt sich für den Auftriebsbeiwert der Tragfläche: c_A = (2 * m * cos φ) / (ρ * F * R * sin θ)
    Zur Findung von R in obiger Gleichung, neben anderen, auch die Werte des "Sperber": G = 1,07 kg, m = G/g = 0,109, F = 0,395 m², ρ = 0,125 kg/s², φ = 5°, θ = 30° und Qw = Quadratwurzel.
    Für den engstmöglichen Radius R_min bei maximalen Auftriebsbeiwert sei c_A = 1,1 knapp vor dem Strömungsabriß: R_min = (2 * 0,109 * 0,996) / (1,1 * 0,125 * 0,395 * 0,5) = 8,0 m.
     Für den Kreisradius mit einem Auftriebsbeiwert c_A = 0,5, also eines Wertes weit unterhalb des Strömungsabrisses, gilt: R = (2 * 0,109 * 0,996) / (0,5 * 0,125 * 0,395 * 0,5) = 17,6 m.
    Die Geschwindigkeit v ergibt sich aus A = G cos φ / cos θ und aus A = Ρ / 2 * c_A * F * v². Aus diesen Gleichungen gilt für v = Qw ((2 * G cos φ) / (Ρ * c_A * F * cos θ)).
     Beispiel 1 zu R_min: v = Qw ((2 * 1,07 * 0,996) / (0,125 * 1,1 * 0,395 * 0,866)) = 6,73 m/s
     Beispiel 2 zu R: v = Qw ((2 * 1,07 * 0,996) / (0,125 * 0,5 * 0,395 * 0,866)) = 9,98 m/s und für die Auftriebskraft A = Ρ / 2 * c_A * F * v²:
Beispiel 1: A = (0,125 / 2) * 1,1 * 0,395 * 6,73² = 1,229 kg. Erforderliche zusätzliche Auftriebserhöhung = 0,159 kg = 14,8 % von 1,07
     Beispiel 2: A = (0,125 / 2) * 0,5 * 0,395 * 9,98² = 1,229 kg.
     ¹) für aufschlussreiche Studien zu diesen und ähnlichen Problemen, kann das Lehrbuch "Design, Leistung und Dynamik von Segelflugmodellen" von Helmut Quabeck unter www.hq-modellflug.de bestellt werden.

     Zusatzbemerkung: beim Freiflugmodell galt, dass im Unterschied zur Trimmung im Geradeausflug, das Modell für den Kreisflug auf Schwanzlastigkeit zurückgetrimmt werden musste, sonst wäre mit der Geradeausflugtrimmung der beginnende Kreisflug nach dem Ausklinken im Hochstart mit einem zu kleinen c_A zu schnell geworden, was schließlich zu schlechten Sinkgeschwindigkeits-Werten geführt hätte. Später stellte ich meine F1A-Modelle so ein: linkes Ohr durch Verwindung positiv angestellt. Der an dieser Stelle erhöhte Auftrieb verlangsamt die örtliche Fluggeschwindigkeit und zwingt das Modell zum Linkskreis, sorgt aber gleichzeitig für den im Kreisflug zusätzlich erforderlichen Auftrieb. Resultat: sehr schöne Flachkreise. Für das benötigte Geradeaussteigen im Hochstart, wurde als Ausgleichs- und Gegenkraft, mit der Hochstartmechanik, ein wenig rechtes Seitenruder eingestellt.
     Eigentlich lag es auch nahe, den "Ur-Sperber" mit Turbulatoren auszurüsten, um herauszufinden, ob damit die kritische Re-Zahl herabgesetzt werden kann und so von vornherein irgendwelche Auslöser zur Strömungsverschlechterung erst gar nicht wirksam werden zu lassen Nach K. Kraemer/Göttingen bewirkt ein Turbulator z.B. beim dem bekannten Profil Gö 801 eine Herabsetzung der kritischen Re-Zahl von Re_krit = 6 * 10⁴ auf Re_krit = 3 * 10⁴ (30.000)! Leider schlugen beim "Ur-Sperber" alle diesbezüglichen Bemühungen, vom üblichen Vorspannturbulator über Wollfaden auf der Fläche bis zu Invigoratoren fehl. Die Ursache dürfte beim elliptischen Grundriss liegen, für dessen unterschiedlichste Flügeltiefen eine Turbulatoranpassung äußerst problematisch zu bewerkstelligen ist. Hier tritt die schon lange gehegte Vermutung wieder auf, dass sich unzweckmäßige Turbulatoren auf die gerade noch überkritisch anliegende Grenzschicht im Geradeausflug negativ auswirken. Sie produzieren eher mehr Widerstand, als dass sie imstande wären, Re_krit positiv zu beeinflussen.

Literaturhinweise: K. Kraemer, "Flügelprofile im kritischen Reynoldszahl-Bereich"
                     Sonderdruck aus der Zeitschrift "Forschung auf dem Gebiet des Ingenieurwesens"
                     H. Quabeck, "Design, Leistung und Dynamik von Segelflugmodellen"
                     HQ Modellflugliteratur Babenhausen
                     F.W. Schmitz "Aerodynamik des Flugmodells"
                     Carl Lange Verlag Duisburg

*Für Freunde des Antikmodellflugs einiges über die Person Helmut Wechler:
Paul Hucke, der Archivar der "Antik Modellflugfreunde Deutschland e.V.", überließ uns freundlicherweise eine Denkschrift über Helmut Wechler, die der Historie wegen hier gerne auszugsweise wiedergegeben wird:

    Nachdem vor allem Mitglieder des "Jüngeren Alters" nachfragen könnten, wer Helmut Wechler war, soll ein kurzer Abriss seines Wirkens dargestellt werden.
    Helmut Wechler wurde am 6. Juni 1909 in Görlitz (Schlesien) geboren. Schon als Schüler galt sein besonderes Interesse dem Zeichnen, der Malerei und flugtechnischen Dingen. Nach dem Abitur (1928) besuchte er die Kunstakademie in Breslau und studierte noch Mathematik an der Universität in Berlin. In den Semesterferien führten ihn weite Studienreisen (mit dem Fahrrad) zu den Kunstwerken in Italien und Frankreich: immer alleine! Dem abgelegten Examen folgte Schuldienst an höheren Lehranstalten in Berlin und Weißwasser in der Oberlausitz.
    Helmut Wechler hatte, wie schon erwähnt, von jeher eine Leidenschaft für die Fliegerei. Segelflugschulung und Prüfung am Hessel- und Hornberg brachten ihm das C-Abzeichen, welches er bis zum Tode trug. Schon bald wurde er für einige Jahre an die Reichsmodellbauschule (RMBS) Rothenburg o.d.Tauber - später nannte man sie Reichsmodellflugschule (RMFS) - berufen. Hier entstanden die von ihm entworfenen Segelflugmodelle "Silbermöve"- We 366, "Sperber"- We 371 und "Reiher"- We 391, Letzteres in Metallbauweise. Als kurze Erklärung sei gesagt, dass bei den Modellnamen der Zusatz z.B. We 366, folgendes bedeutet: We für Wechler und 366, das 6. Modell im Jahre 1936. Von diesen Modellen erschienen beim Moritz Schäfer-Verlag in Leipzig auch Baupläne. Manche Gedanken über den Flugmodellbau veröffentlichte er auch in der einschlägigen Literatur.
    Kriegsdienst bei der Luftwaffe und Gefangenschaft blieben auch ihm nicht erspart. Schließlich wurde er mit seiner Familie, 1948, in Marktredwitz, heimisch. Hier unterrichtete er am Gymnasium Mathematik und Zeichnen. 1974 ging er als Studiendirektor in Pension. Jetzt malte Helmut Wechler wieder und reiste, jedoch nicht mit dem Fahrrad, zu den antiken Kunstschätzen. Gelegentlich flog er gern in Segelflugzeugen oder Motorseglern sogar über Land mit. Leises Gleiten, Schweben, Steigen, erfreuten sein Herz immer wieder von neuem.
    Leider musste uns Helmut Welcher am 14. Dezember 1992, jedoch im stattlichen Alter von 83 Jahren, für immer verlassen.
    Seine Konstruktionen, allem voran der "Sperber", werden weitergebaut und so bleibt er immer in unserer Erinnerung. Einer seiner Schüler an der RMFS war der 13 Jahre jüngere Bruder Joachim Wechler. Er ist heute noch der Modellfliegerei platonisch sehr verbunden.